スケジューリング

スケジューリングとはスケジューリング問題とは仕事間の先行関係及び各手順を処理するのに要する資源(人,設備,資金など)が与えられているとき, それらの資源制約をみたしつつ,　総費用や総所要時間などを最小化する問題のことです. これを厳密に解くのは容易ではなく,　短時間で準最適な解を得るためのアルゴリズムの開発が求められています. 最近では, スケジューリングの対象はさまざまな分野へ広がっており, 時間割作成(タイムテーブリング)やスポーツの大会日程作成, 航空機スケジューリング, 医療・看護・介護, 鉄道・交通スケジューリング, 配送スケジューリング, エレベータやビデオの予約スケジューリングなどがあります.

それでは, 本グループの研究について紹介していきます.

1. 鉄道乗務員スケジューリング問題の解法

鉄道乗務員スケジューリング問題とは, 与えられた列車の運行予定に対 して必要な乗務員の配置スケジュールを決定する問題です. 各列車には必ず 一人以上の乗務員を割り当てなければなりません. 乗務員の休憩時間や勤務 スケジュールなどを考慮して, あらゆる制約条件を考慮した乗務員スケジュー ルを作成することを目的としています. また, 列車ダイヤが乱れた条件下で も, 対応できるような乗務員スケジューリングが求められています.

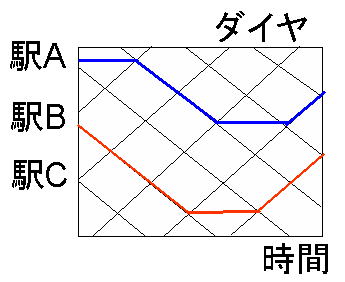
列車ダイヤと乗務員スケジュールの例

2. 生産スケジューリング

ある製品が複数の工程を通って最終製品になるとき, すべでの工程順序が同一の条件ですべての工程での作 業の先行関係を満たして, 機械での作業の重複のないスケジュールを決定する問題をフローショップ問題と呼びます. 現実の工場のスケジューリング問題の多くはフローショップスケジューリング問題として扱うことができます. 各製品の納期が与えられたとき, 納期遅れを最小とするフローショップスケジューリング問題は一見やさしいように思われますが, 最適化解を得ることは容易ではありません. このように一般化された問題に対する効率の良いアルゴリズムの開発を行っています.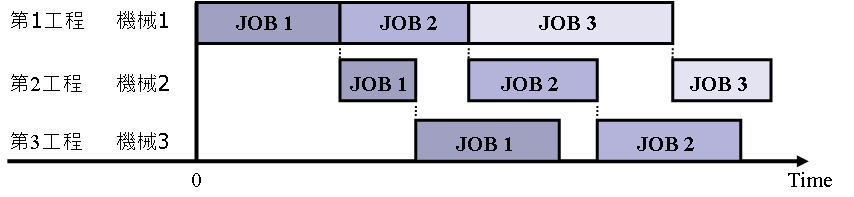
フローショップスケジューリングの例

3.　ラグランジュ分解調整法の拡張

ラグランジュ分解調整法と呼ばれる近似解法解で得た解をさらに改善していくため, 新しいアルゴリズムの開発を進めている. カラムジェネレーション（列生成法）やカッティングプレーン（切除平面法), 拡張ラグランジュ法などを用いて, 双対問題の解と主問題の解のギャップをなくすことができる手法の開発をめざしています.